Sunday, April 30, 2017
Paradise ponders: router table and sushi edition...
A wall around California...
A wall around California... I suspect the majority of the population of the Mountain States would think this was a very good idea!
Saturday, April 29, 2017
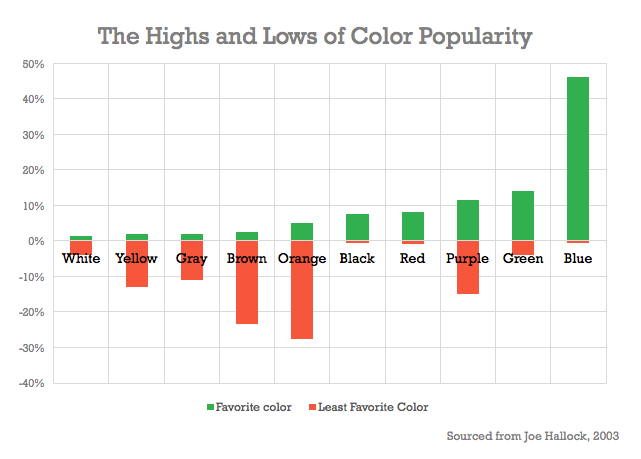
Favorite colors...
Favorite colors... It would never have occurred to me to study the question of what colors are people's favorites. Nor would I have expected that there would be significant differences in the popularity of various colors. But there apparently are:
My own favorite color? Well, I'd have a hard time choosing between bright orange (like a California poppy) or bright yellow (like a nice lemon). Maybe a slight preference to the orange. That puts me solidly in the weirdo category, it seems. One of my friends likes to call me “six sigmas” because I'm at least six standard deviations from normal (though I claim eight!). This seems to be yet another dimension in which I deviate... :)
Paradise ponders: Utah gratitude edition...
Paradise ponders: Utah gratitude edition... I fled to Utah from California just three years ago, after living in that sunny land for 43 years. When I first came to California, in 1971, I was coming from New Jersey. The California of 1971 was a paradise by comparison to the hell-on-earth that was New Jersey. Back then, even California's government was better.
It was all downhill from there. By the time we retired in 2013, it was obvious to Debbie and I that our long-planned retirement in the mountains of San Diego wasn't going to be the dream we'd thought it would be. We made up our minds to leave, and we chose Utah for many reasons.
It turns out, though, that we'd underestimated (by a lot!) just how well we'd fit in here in Utah. We'd expected the natural beauty, as we'd traveled here many times. We knew the weather would include actual seasons. We hoped that the government would prove to be less intrusive, more common-sensical, and it has. But we did not expect the people here to be so welcoming, despite our not being of the predominant faith here (LDS). We also didn't expect some other things, slightly subtler, but that turn out to be very important to us.
I'd say the biggest one, for me, is the general assumption of honesty here. In general, people just trust one another. If you tell a craftsman that you agree with their price, they'll just proceed with the work and trust that you'll pay them. If you leave your wallet somewhere, you can trust that it will be held for you, contents intact. If you leave your car unlocked, you can trust that it will not be stolen. If you carry ten items to the cash register in a store and tell the clerk you have ten of them, she'll just ring you up for ten without even counting. And so on. I'm talking about out here in the countryside, where we live – the story is different in the cities, of course. Out here, though, people just assume that you're honest in your dealings. How refreshing, especially compared with our experiences in California!
Another slightly subtle surprise for us: we can depend on others around here for help, and they assume they can depend on us. I still get surprised by this quite often – people are all the time volunteering to help out, and they really mean it.
And some of our neighbors have become good friends, despite the vast differences in our backgrounds and experiences.
We're very grateful for the wonderful home that Utah has made for us.
And when we read things about California, like this or this, we're even more grateful for Utah providing us with refuge!
It was all downhill from there. By the time we retired in 2013, it was obvious to Debbie and I that our long-planned retirement in the mountains of San Diego wasn't going to be the dream we'd thought it would be. We made up our minds to leave, and we chose Utah for many reasons.
It turns out, though, that we'd underestimated (by a lot!) just how well we'd fit in here in Utah. We'd expected the natural beauty, as we'd traveled here many times. We knew the weather would include actual seasons. We hoped that the government would prove to be less intrusive, more common-sensical, and it has. But we did not expect the people here to be so welcoming, despite our not being of the predominant faith here (LDS). We also didn't expect some other things, slightly subtler, but that turn out to be very important to us.
I'd say the biggest one, for me, is the general assumption of honesty here. In general, people just trust one another. If you tell a craftsman that you agree with their price, they'll just proceed with the work and trust that you'll pay them. If you leave your wallet somewhere, you can trust that it will be held for you, contents intact. If you leave your car unlocked, you can trust that it will not be stolen. If you carry ten items to the cash register in a store and tell the clerk you have ten of them, she'll just ring you up for ten without even counting. And so on. I'm talking about out here in the countryside, where we live – the story is different in the cities, of course. Out here, though, people just assume that you're honest in your dealings. How refreshing, especially compared with our experiences in California!
Another slightly subtle surprise for us: we can depend on others around here for help, and they assume they can depend on us. I still get surprised by this quite often – people are all the time volunteering to help out, and they really mean it.
And some of our neighbors have become good friends, despite the vast differences in our backgrounds and experiences.
We're very grateful for the wonderful home that Utah has made for us.
And when we read things about California, like this or this, we're even more grateful for Utah providing us with refuge!
Friday, April 28, 2017
Paradise ponders: snow and router table edition...
Paradise ponders: snow and router table edition... The router table is now complete except for the actual router and it's lifter (they're supposed to arrive today). The rest of the kit went together just as perfectly as the first third. The only challenging part turned out to be putting that cast iron top on. That thing was heavy (I'm guessing about 70 pounds), and the bolts that attach it to the stand go up through the bottom of it. That was a real booger to get on, because the top's mounting holes had to be precisely aligned with the corresponding holes in the stand, and because I couldn't see a darned thing inside the cabinet (no space to get my fat head in there). The first photo below shows the wood chip box that's supposed to make this router table nearly dust and chip free. We'll see how well that works!
Our weather today is really hard to believe for being nearly May. We've had rain, hail, sleet, and snow today, all day long. Right now it's raining. It's about 35°F outside, so the snow and sleet aren't sticking very long, thankfully. Our trees (at right) had some snow on their leaves, though. But once again, it's wet as heck outside – there's mud everywhere. Dang.
AI and deep learning...
AI and deep learning... My long time readers will know that I am very skeptical of artificial intelligence (AI) in general. By that I mean two separate things these days, as the field of AI has split into two rather different things the past few years.
The first (and oldest) meaning was the general idea of making computers “intelligent” in generally the same way as humans are intelligent. Isaac Asimov's I, Robot stories and their derivatives perfectly illustrated this idea. The progress researchers have made on this sort of AI is roughly the same as the progress they've made on faster-than-light space travel: nil. I am skeptical that they ever will, as everything I know about computers and humans (more about the former than the latter!) tells me that they don't work the same way at all.
The second more recent kind of AI is generally known by the moniker “deep learning”. I think that term is a bit misleading, but never mind that. For me the most interesting thing about deep learning is that nobody knows how any system using deep learning actually works. Yes, really! In this sense, deep learning systems are a bit like people. An example: suppose spent a few days learning how to do something new – say, candling eggs. You know what the process of learning is like, and you know that at the end you will be competent to candle eggs. But you have utterly no idea how your brain is giving you this skill. Despite this, AI researchers have made enormous progress with deep learning. Why? Relative to other kinds of AI, it's easy to build. It's enabled by powerful processors, and we're getting really good at building those. And, probably most importantly, there are a large number of relatively simple tasks that are amenable to deep learning solutions.
Deep learning systems (which are programs, sometimes running on special computers) we know how to train, but we don't know how the result works, just like with people. You go through a process to train them how to do some specific task, and then (if you've done it right) they know how to do it. What's fascinating to me as a programmer is that no programming was involved in teaching the system how to do its task – just training of a general purpose deep learning system. And there's a consequence to that: no programmer (or anyone else) knows how that deep learning system actually does its work. There's not even any way to figure that out.
There are a couple of things about that approach that worry me.
First, there's the problem of how that deep learning system will react to new inputs. There's no way to predict that. My car, a Tesla Model X, is a great example of such a deep learning system. It uses machine vision (a video camera coupled with a deep learning system) to analyze the road ahead and decide how to steer the car. In my own experience, it works very well when the road is well-defined by painted lines, pavement color changes, etc. It works much less well otherwise. For instance, not long ago I had it in “auto-steer” on a twisty mountain road whose edges petered off into gravel. To my human perception, the road was still perfectly clear – but to the Tesla it was not. Auto-steer tried at one point to send me straight into a boulder! :) I'd be willing to bet you that at no time in the training of its deep learning system was it ever presented with a road like the one I was on that day, and therefore it really didn't know what it was seeing (or, therefore, how to steer). The deep learning method is very powerful, but it's still missing something that human brains are adding to that equation. I suspect it's related to the fact that the deep learning system doesn't have a good geometrical model of the world (as we humans most certainly do), which is the subject of the next paragraph.
Second, there's the problem of insufficiency, alluded to above. Deep learning isn't the only thing necessary to emulate human intelligence. It likely is part of the overall human intelligence emulation problem, but it's far from the whole thing. This morning I ran across a blog post talking about the same issue, in this case with respect to machine vision and deep learning. It's written by a programmer who works on these systems, so he's better equipped to make the argument than I am.
I think AI has a very long way to go before Isaac Asimov would recognize it, and I don't see any indications that the breakthroughs needed are imminent...
The first (and oldest) meaning was the general idea of making computers “intelligent” in generally the same way as humans are intelligent. Isaac Asimov's I, Robot stories and their derivatives perfectly illustrated this idea. The progress researchers have made on this sort of AI is roughly the same as the progress they've made on faster-than-light space travel: nil. I am skeptical that they ever will, as everything I know about computers and humans (more about the former than the latter!) tells me that they don't work the same way at all.
The second more recent kind of AI is generally known by the moniker “deep learning”. I think that term is a bit misleading, but never mind that. For me the most interesting thing about deep learning is that nobody knows how any system using deep learning actually works. Yes, really! In this sense, deep learning systems are a bit like people. An example: suppose spent a few days learning how to do something new – say, candling eggs. You know what the process of learning is like, and you know that at the end you will be competent to candle eggs. But you have utterly no idea how your brain is giving you this skill. Despite this, AI researchers have made enormous progress with deep learning. Why? Relative to other kinds of AI, it's easy to build. It's enabled by powerful processors, and we're getting really good at building those. And, probably most importantly, there are a large number of relatively simple tasks that are amenable to deep learning solutions.
Deep learning systems (which are programs, sometimes running on special computers) we know how to train, but we don't know how the result works, just like with people. You go through a process to train them how to do some specific task, and then (if you've done it right) they know how to do it. What's fascinating to me as a programmer is that no programming was involved in teaching the system how to do its task – just training of a general purpose deep learning system. And there's a consequence to that: no programmer (or anyone else) knows how that deep learning system actually does its work. There's not even any way to figure that out.
There are a couple of things about that approach that worry me.
First, there's the problem of how that deep learning system will react to new inputs. There's no way to predict that. My car, a Tesla Model X, is a great example of such a deep learning system. It uses machine vision (a video camera coupled with a deep learning system) to analyze the road ahead and decide how to steer the car. In my own experience, it works very well when the road is well-defined by painted lines, pavement color changes, etc. It works much less well otherwise. For instance, not long ago I had it in “auto-steer” on a twisty mountain road whose edges petered off into gravel. To my human perception, the road was still perfectly clear – but to the Tesla it was not. Auto-steer tried at one point to send me straight into a boulder! :) I'd be willing to bet you that at no time in the training of its deep learning system was it ever presented with a road like the one I was on that day, and therefore it really didn't know what it was seeing (or, therefore, how to steer). The deep learning method is very powerful, but it's still missing something that human brains are adding to that equation. I suspect it's related to the fact that the deep learning system doesn't have a good geometrical model of the world (as we humans most certainly do), which is the subject of the next paragraph.
Second, there's the problem of insufficiency, alluded to above. Deep learning isn't the only thing necessary to emulate human intelligence. It likely is part of the overall human intelligence emulation problem, but it's far from the whole thing. This morning I ran across a blog post talking about the same issue, in this case with respect to machine vision and deep learning. It's written by a programmer who works on these systems, so he's better equipped to make the argument than I am.
I think AI has a very long way to go before Isaac Asimov would recognize it, and I don't see any indications that the breakthroughs needed are imminent...
Paradise ponders: of ovens and arduous kits...
I'm about one third of the way through the assembly, and so far I am very pleasantly surprised. With just a single exception, every part has fit precisely correctly, first try. Better yet, the edges of the sheet metal don't seem quite so sharp – no cuts yet (and no bloodstains on the goods!). The one exception was a minor one: I needed one gentle tap of the rubber mallet to get a recalcitrant threaded hole to line up with a drilled hole. The directions are crystal clear, with great illustrations. I hope the rest of the assembly is just as nice!
Thursday, April 27, 2017
NASA at...
NASA at ... its most awesome, and at its least awesome... Too bad there's so much more of the latter than the former...
Paradise ponders: artichokes, kits, better indexes, and electricity edition...
Over the past few days some tools I've ordered arrived: a couple of jigs (for making box joints and mortise-and-tenon joints) and a router table. All three of these are kits – boxes of parts with bags of nuts and bolts. Big bags of nuts and bolts. I'm gonna be putting things together for a while before I can use them. All three of these were long-planned, but I need them now to let me build some stuff for the cattery. Somehow I didn't expect the jigs to be kits, but the fact that the router table is a kit doesn't really surprise me...
A couple days ago I posted about an index to look up the value of the largest decimal digit that is smaller than a given binary value. The code that I posted was ... not optimal. Here's a better attempt:
In addition to a better algorithm, I also made the code easier to read. The compiler optimizes the local variables away, so there's no performance impact to this. The 9 bit index generated is pretty simple. If 2^k is the most significant bit in _val, then the upper six bits of the index are k, and the lower three bits are the bits in _val at 2^k-1, 2^k-2, and 2^k-3 (with a bit of special casing for k < 3).int lz = Long.numberOfLeadingZeros( _val ); int mag = 63 - lz; int hi = mag << 3; long sec = Long.highestOneBit( _val ) ^ _val; int lo = (int)(sec >>> Math.max(0, mag - 3)); int index = hi | lo;
I'm going to be putting up a little shed soon, to house some components of our sprinkler system. I had my favorite electrician (Tyler, from Golden Spike Electric) out yesterday evening to check out the job. It's such a pleasure to work with people like him! I want something kind of weird (naturally!), and he had absolutely no problem accommodating me. I'm going to have him run a 50 amp 220 volt circuit to a subpanel in the new shed, and I'm going to wire it from there. “No problem”, says he – and we looked over the existing panel that he'd connect to. There was a circuit installed long ago that ran to an external plug for an RV. This is not something we'll ever need, so we're going to remove that and steal the existing breaker (which happens to be 50 amp!) for my new subpanel. Easy peasy!
Wednesday, April 26, 2017
Paradise ponders: Debbie's “graduation”, filling station milestone, steam train, and tax cuts...
Paradise ponders: Debbie's “graduation”, filling station milestone, steam train, and tax cuts... This morning Debbie went in to see her surgeon for a two week post-surgery followup. He pronounced her recovery to be great, ready to get her staples taken out, and cleared for any physical activity that didn't cause her pain. She looked so good, in fact, that he declared it unnecessary for her to have the usual subsequent followup visits. This prompted a nurse who was in the room to comment that Debbie had “graduated”. Yay! The staples came out (something that Debbie really hates – she crushed my hand and buried her head in my shoulder while the nurse did this), and now her big job is to see how far she can push herself with exercise before it gets painful. First milestone there will be walking without any walker, crutches, or cane. The surgeon said she could be doing this just as soon as she can comfortably put full weight on her left knee.
Yesterday the guys were here working on our filling station. They got all the pipe cut, threaded, and installed – the tanks are now actually connected to the nozzles! I just put in a call to my fuel supplier, and within a few days I should actually have some gasoline and diesel fuel sloshing around in those tanks. There's still more work to do on the filling station, but we can use it while that work gets done. I've just ordered the steel door to go in the front of it; that should be here in six weeks or so. I've also got Randy Bingham (the mason who did our fireplace) lined up to put rock on top and all around it, but it might be a while before that gets done. Progress!
Yesterday we'd planned to go see a steam locomotive that was scheduled to stop for just a half hour in Cache Valley. The place where it was to stop was the teensy little town of Cache Junction, just south of my brother Scott's home. This town has about four houses, and it's kind of in the boonies of Cache Valley – so we weren't expecting many people to show up for it. Man, were we wrong! There were a couple hundred cars parked there, overflowing the little parking area to line the sides of the roads for a half mile or so on both sides of town. I'd guess that around a thousand people were milling all about. In that environment there was no way for us to park close by for a view of the train, and Debbie's not ready to walk over rough ground, so we just drove through town and marveled at the size of the crowd. We visited for a little while with my brother (where we picked up some beautiful logs he'd saved for me) and on the way out we did get to see the locomotive as it approached Cache Junction. We crossed the tracks about 2 miles from Cache Junction and were amused to see that a crowd had gathered there as well. This steam locomotive was darned popular here!
As I started writing this post, news is trickling in about Trump's proposed tax cut. I have no idea what the chances are that this will actually get through Congress intact, but I'm skeptical given the magnitude of the cuts and the general hostility of the Democrats. But one aspect of the proposed plan jumped out at me: repealing the federal income tax deduction for state and local taxes. This deduction is, in effect, a federal subsidy that disproportionately benefits residents of high tax states. I'd be delighted to see that actually be repealed, but it's easy to foresee that the Democrats will start crazed howling about this one. That's so obvious that I have to wonder if it was included in the proposal mainly as a sop whose removal could be traded for Democratic votes in the Senate...
Yesterday the guys were here working on our filling station. They got all the pipe cut, threaded, and installed – the tanks are now actually connected to the nozzles! I just put in a call to my fuel supplier, and within a few days I should actually have some gasoline and diesel fuel sloshing around in those tanks. There's still more work to do on the filling station, but we can use it while that work gets done. I've just ordered the steel door to go in the front of it; that should be here in six weeks or so. I've also got Randy Bingham (the mason who did our fireplace) lined up to put rock on top and all around it, but it might be a while before that gets done. Progress!
Yesterday we'd planned to go see a steam locomotive that was scheduled to stop for just a half hour in Cache Valley. The place where it was to stop was the teensy little town of Cache Junction, just south of my brother Scott's home. This town has about four houses, and it's kind of in the boonies of Cache Valley – so we weren't expecting many people to show up for it. Man, were we wrong! There were a couple hundred cars parked there, overflowing the little parking area to line the sides of the roads for a half mile or so on both sides of town. I'd guess that around a thousand people were milling all about. In that environment there was no way for us to park close by for a view of the train, and Debbie's not ready to walk over rough ground, so we just drove through town and marveled at the size of the crowd. We visited for a little while with my brother (where we picked up some beautiful logs he'd saved for me) and on the way out we did get to see the locomotive as it approached Cache Junction. We crossed the tracks about 2 miles from Cache Junction and were amused to see that a crowd had gathered there as well. This steam locomotive was darned popular here!
As I started writing this post, news is trickling in about Trump's proposed tax cut. I have no idea what the chances are that this will actually get through Congress intact, but I'm skeptical given the magnitude of the cuts and the general hostility of the Democrats. But one aspect of the proposed plan jumped out at me: repealing the federal income tax deduction for state and local taxes. This deduction is, in effect, a federal subsidy that disproportionately benefits residents of high tax states. I'd be delighted to see that actually be repealed, but it's easy to foresee that the Democrats will start crazed howling about this one. That's so obvious that I have to wonder if it was included in the proposal mainly as a sop whose removal could be traded for Democratic votes in the Senate...
Tuesday, April 25, 2017
Binary to decimal conversion performance...
Binary to decimal conversion performance... Now here's an obscure topic that I've worked on a great many times over my career. The original inspiration for me to work on this came from programming the Z-80, way back in the '70s. That little 8 bit microprocessor could do 16 bit addition, but it had no multiply or divide instructions at all. Often the application I was working on needed higher precision math (usually 32 bits), so I had a library of assembly language subroutines that could do the basic four 32 bit operations: add, subtract, multiply, and divided. Multiply and divide were maddeningly slow. Eventually I came up with a way to speed up multiply considerably, but divide was intractably slow.
This slow divide performance was on full display anytime I wanted to convert a 32 bit binary integer to its decimal equivalent. The canonical algorithm uses repeated division-with-remainder by ten. For instance, to convert the binary number 11001001 to its decimal equivalent, you would do this:
What I came up with has been independently invented by many people; I wasn't the first, I'm sure, and I don't know who was. The basic technique depends on a simple observation: there aren't all that many possible decimal digits whose value fits in a given length binary number. For instance, in a signed 32 bit binary number, the largest positive decimal number that can be represented is 2,147,483,647. That's 10 decimal digits, any of which can have the non-zero values [1..9], except the most significant one can only be [1..2]. That's just 83 values. If you pre-compute all those 83 values and put them in a table, then you can convert a binary number to decimal with this algorithm:
That was vital to getting decent performance out of that Z-80. But what about a modern processor? Well, it turns out that in relative terms, division is still the red-haired stepchild of CPU performance. On a modern Intel or ARM processor, 64 bit integer division can take over 100 CPU clock cycles. Multiply operations, by comparison, take just a handful of clock cycles, while addition and subtraction are generally just 1 or 2 clock cycles. Even when using a high-level language like Java, algorithms that avoid using division repetitively can still produce large performance gains. I've done this five or six times now, most recently to get a 6:1 performance gain when converting floating point values to XML.
One line of the above algorithm I sort of glossed over: the bit about finding the largest value of a decimal digit that is less than the remaining value. The naive way to do this would be to use a linear search, or possibly a binary search of the table of decimal digit values. This would require a number of iterations over the search algorithm, at best an average of 4 iterations for a binary search over a table big enough for 32 bit values. For 64 bit values we'd have 171 decimal digit values, and we'd need 5 iterations for that binary search.
We can do better, though, by taking advantage of the fact that there's a close relationship between the binary values and the largest fitting decimal digit. I just finished coding up a nice solution for finding the largest decimal digit that fits into a signed 64 bit integer. It works by using a table with 512 entries, about three times as many as we have possible decimal digit values. Given a 64 bit positive binary number, the Java code that computes the index into that table is:
With those two techniques in combination, I'm doing conversions from binary to decimal with no divisions and no iterative searching. It's very challenging to benchmark performance in Java, but my simple testing shows about 5:1 improvement in performance for random numbers in the 64 bit positive integer range. Smaller numbers (with fewer decimal digits) show smaller performance gains, but always at least 2:1. I'll call that a win!
This slow divide performance was on full display anytime I wanted to convert a 32 bit binary integer to its decimal equivalent. The canonical algorithm uses repeated division-with-remainder by ten. For instance, to convert the binary number 11001001 to its decimal equivalent, you would do this:
11001001 / 1010 = 10100 remainder 1The result is then the remainders, in decimal, in reverse order: 201. You need one division operation for each digit of the result. A 32 bit number might have as many as ten digits, and on that low-horsepower little Z-80, those divisions were really expensive. So I worked hard to come up with an alternative means of conversion that didn't require division.
10100 / 1010 = 10 remainder 0
10 / 1010 = 0 remainder 10
What I came up with has been independently invented by many people; I wasn't the first, I'm sure, and I don't know who was. The basic technique depends on a simple observation: there aren't all that many possible decimal digits whose value fits in a given length binary number. For instance, in a signed 32 bit binary number, the largest positive decimal number that can be represented is 2,147,483,647. That's 10 decimal digits, any of which can have the non-zero values [1..9], except the most significant one can only be [1..2]. That's just 83 values. If you pre-compute all those 83 values and put them in a table, then you can convert a binary number to decimal with this algorithm:
start with the binary value to be convertedThis produces the decimal digits in order, from the most significant digit to the least significant digit. Most importantly, it does so with no division required.
while remaining value is nonzero
find the largest value of a decimal digit < the remaining value
record the digit
subtract that decimal digit value from the remaining value
That was vital to getting decent performance out of that Z-80. But what about a modern processor? Well, it turns out that in relative terms, division is still the red-haired stepchild of CPU performance. On a modern Intel or ARM processor, 64 bit integer division can take over 100 CPU clock cycles. Multiply operations, by comparison, take just a handful of clock cycles, while addition and subtraction are generally just 1 or 2 clock cycles. Even when using a high-level language like Java, algorithms that avoid using division repetitively can still produce large performance gains. I've done this five or six times now, most recently to get a 6:1 performance gain when converting floating point values to XML.
One line of the above algorithm I sort of glossed over: the bit about finding the largest value of a decimal digit that is less than the remaining value. The naive way to do this would be to use a linear search, or possibly a binary search of the table of decimal digit values. This would require a number of iterations over the search algorithm, at best an average of 4 iterations for a binary search over a table big enough for 32 bit values. For 64 bit values we'd have 171 decimal digit values, and we'd need 5 iterations for that binary search.
We can do better, though, by taking advantage of the fact that there's a close relationship between the binary values and the largest fitting decimal digit. I just finished coding up a nice solution for finding the largest decimal digit that fits into a signed 64 bit integer. It works by using a table with 512 entries, about three times as many as we have possible decimal digit values. Given a 64 bit positive binary number, the Java code that computes the index into that table is:
Pretty simple code, really. It's also very fast. Best of all, with a properly constructed table the index will point to an entry that will either be the correct one (that is, the largest decimal digit that will fit into the value) or it will be too big. If it is too big, then the preceding entry in the table is guaranteed to be the correct one. Much better than the iterative searches!int lz = Long.numberOfLeadingZeros( value ); int index = ((63 - lz) << 3) + (0xf & (int)Long.rotateRight( value, 60 - lz));
With those two techniques in combination, I'm doing conversions from binary to decimal with no divisions and no iterative searching. It's very challenging to benchmark performance in Java, but my simple testing shows about 5:1 improvement in performance for random numbers in the 64 bit positive integer range. Smaller numbers (with fewer decimal digits) show smaller performance gains, but always at least 2:1. I'll call that a win!
Monday, April 24, 2017
Paradise ponders: rain, and strange coincidences edition...
This morning I spoke for a little while with the attorney I'm using to handle a real estate transaction in Virginia. He mentioned that he was a little familiar with Utah, as he used to come out here for vacations, especially near Moab. So I shared a bit with him about our numerous trips there, and I mentioned that we knew the La Sal Mountains very well. He then related his happy visits to Pack Creek Ranch, a now-defunct resort on the western slopes of the La Sals. Debbie and I have very happy memories of that place, having stayed there several times ourselves. It's a little bitty resort, way out of the way, exactly our sort of place precisely because it's not very popular. And yet ... this lawyer from Virginia knew it, and had stayed there three or four times. What a bizarre coincidence!
A step taken...
A step taken... This morning I registered a new domain: decinum.org. I was a bit surprised that it hadn't already been taken – my usual experience with finding domain names is that the first 1,000 or so that I try have already been snagged. :) Further, to my amazement, 60 seconds after registering decinum.org, the DNS resolution was already working. The first domain I ever registered (dilatush.com, back in '93) took several days to get that far.
This new registration is a first step for an open source project I'm going to start working on. The main purpose is to actually implement the observations and ideas I've had for representing money in Java. The vast majority of that work lies in representing high precision decimal numbers, hence the domain name. I won't have any web site for decinum.org at first; I locked down the name mainly so I could safely use it for Java class names...
This new registration is a first step for an open source project I'm going to start working on. The main purpose is to actually implement the observations and ideas I've had for representing money in Java. The vast majority of that work lies in representing high precision decimal numbers, hence the domain name. I won't have any web site for decinum.org at first; I locked down the name mainly so I could safely use it for Java class names...
Sunday, April 23, 2017
Paradise ponders, 8' lumber, oven removal, and scallops edition...
Paradise ponders, 8' lumber, oven removal, and scallops edition... Tomorrow we're supposed to get our new oven installed. You may remember that we gave up on our old oven after three failed attempts to get it repaired. The new one is a Bosch model that we're hoping we're just as happy with as we are with our Bosch dishwasher. Also, it came highly recommended by our repair technician.
So this morning I tackled what I thought was likely to be an all-day job: removing the old oven and installing an electrical junction box. The house's previous owner had done an awesomely shabby job of wiring the old oven: he just used wire nuts to join the wires, covering them with approximately eight miles of electrical tape. It's the sort of electrical job you might imagine a child doing. I ran into something similar when I replaced the microwave directly above this oven, and there I had room to install a standard outlet box. The new oven is 220V, and those outlets are way too big to install in the cramped space the oven must fit in. So I went with a hard-wired junction box.
Taking the oven out turned out to be relatively easy. I had the old oven out in our garage just a half hour after starting. With some creative use of our hand truck, it wasn't even all that difficult. The hardest part was getting it onto the hand truck – wrangling 185 lbs of oven by myself was a bit of a challenge! But I got it...
We made a run to Home Depot and got all the electrical parts I needed. Installing them took all of another half hour. So by 10 am I was completely done with that job. Yay!
So we made another run to Home Depot, this time to buy the stuff I needed to build out a couple of frames around two of our basement windows in our cattery. These are the windows that we've opened up to our sun room. I removed the glass sliding windows, including their frame, and now we just have the steel frame that's set into the basement's concrete wall. I'm building a frame out of cedar 1x8's with the boards perpendicular to the plane of the old window. This is at the suggestion of our mason, who will use that frame as one edge of the rock he's installing.
I needed to buy five 8' long pieces of cedar (1x8s), so I did some measuring to see if it would be possible to fit those in our Model X. To my surprise, the answer was yes! About six inches of the boards needed to extend over the center console, which I covered with a shipping pad to protect. The photo at right I took while standing behind the open rear hatch. You can see the “hole” between the two front seats where we stowed the boards, along with the pads I used to protect it. We keep getting surprised by what we can carry in the Model X – it's really quite roomy inside (especially our five seat version with the rear seats folded down).
On the way to Home Depot, I stopped for a few groceries at Smith's. That's not where we usually shop, so while I was in there I did a little scouting. On the way by the seafood counter I spotted scallops – the great, big sea scallops that Debbie uses in her scrumptious baked scallops recipe. I bought a pound and a half, and Debbie is cooking them as I write this. Feast today!
So this morning I tackled what I thought was likely to be an all-day job: removing the old oven and installing an electrical junction box. The house's previous owner had done an awesomely shabby job of wiring the old oven: he just used wire nuts to join the wires, covering them with approximately eight miles of electrical tape. It's the sort of electrical job you might imagine a child doing. I ran into something similar when I replaced the microwave directly above this oven, and there I had room to install a standard outlet box. The new oven is 220V, and those outlets are way too big to install in the cramped space the oven must fit in. So I went with a hard-wired junction box.
Taking the oven out turned out to be relatively easy. I had the old oven out in our garage just a half hour after starting. With some creative use of our hand truck, it wasn't even all that difficult. The hardest part was getting it onto the hand truck – wrangling 185 lbs of oven by myself was a bit of a challenge! But I got it...
We made a run to Home Depot and got all the electrical parts I needed. Installing them took all of another half hour. So by 10 am I was completely done with that job. Yay!
So we made another run to Home Depot, this time to buy the stuff I needed to build out a couple of frames around two of our basement windows in our cattery. These are the windows that we've opened up to our sun room. I removed the glass sliding windows, including their frame, and now we just have the steel frame that's set into the basement's concrete wall. I'm building a frame out of cedar 1x8's with the boards perpendicular to the plane of the old window. This is at the suggestion of our mason, who will use that frame as one edge of the rock he's installing.
On the way to Home Depot, I stopped for a few groceries at Smith's. That's not where we usually shop, so while I was in there I did a little scouting. On the way by the seafood counter I spotted scallops – the great, big sea scallops that Debbie uses in her scrumptious baked scallops recipe. I bought a pound and a half, and Debbie is cooking them as I write this. Feast today!
Saturday, April 22, 2017
Jaw-dropping innumeracy test...
Jaw-dropping innumeracy test... I ran across this online somewhere (can't find it now), read their results and suspected shenanigans. I was wrong. In fact, my own tests suggest the innumeracy situation might even be worse than the report I read.
Here's the test:
So I've tried the test now on five people (a ludicrously small sample, I know), more or less randomly selected. None of them were even remotely close to the right answer. The most common place for the third dot was somewhere near the middle of the line. One person put it about 1/5th of the line's length from the right! I'm slightly comforted by the fact that none of these people were scientists or engineers ... but only slightly comforted.
I find this absolutely stunning. Somehow it never occurred to me that so many adults – probably a majority of adults – wouldn't intuitively grasp such basic concepts. That level of innumeracy means that things like discussions of government budgets are beyond their ken, as they don't understand the significance of the difference between millions, billions, or trillions of dollars (and probably not thousands, either!). Or basic astronomical concepts. Sheesh, much of science involves numbers covering multiple orders of magnitude.
Gobsmacked, I am...
Here's the test:
Take a piece of blank paper. Draw a dot on the left and mark it “0”. Draw a dot opposite the first one, on the right, and mark it “1,000,000,000” (one billion). Draw a line between the two dots. That's a number line, like many of us learned in school. It represents all the numbers between zero and a billion, with the integers equally spaced. Now draw a third dot on the line where you think the number 1,000,000 (one million) belongs.The report I read said that about half of people trying this test put the third dot in roughly the correct place; everyone else got it wrong. That's the result I was skeptical of. The correct place, of course, is 1/1000th of the line's length from the left. So if your line was 10 inches long, the third dot would be a mere 1/100th of an inch from the dot for zero.
So I've tried the test now on five people (a ludicrously small sample, I know), more or less randomly selected. None of them were even remotely close to the right answer. The most common place for the third dot was somewhere near the middle of the line. One person put it about 1/5th of the line's length from the right! I'm slightly comforted by the fact that none of these people were scientists or engineers ... but only slightly comforted.
I find this absolutely stunning. Somehow it never occurred to me that so many adults – probably a majority of adults – wouldn't intuitively grasp such basic concepts. That level of innumeracy means that things like discussions of government budgets are beyond their ken, as they don't understand the significance of the difference between millions, billions, or trillions of dollars (and probably not thousands, either!). Or basic astronomical concepts. Sheesh, much of science involves numbers covering multiple orders of magnitude.
Gobsmacked, I am...
Paradise ponders, brief “I’m busy!” edition...
Paradise ponders, brief “I’m busy!” edition... Yesterday none of our workers showed up, and no progress was made on any project. I hate days like that!
I squired Debbie down to Ogden for her hair appointment, which took 3.5 hours. She does this every five weeks, so that works out to roughly 40 hours a year. Me, I get a haircut every 5 or 6 months, whether I need it or not. :) My haircuts generally take less than 15 minutes. My haircuts cost $15, including a 50% tip (which the ladies who cut my hair are very happy with!). Debbie's cost ... you don't want to know, especially if you include the cost of the chemical soup she buys to maintain it. Now, I like her hair, mind you. I'm just noting the differences here, and pondering the magnitude of the investment of time and treasure. I cannot even imagine doing this myself...
When we were done with her hair appointment, we tried out a new restaurant in Ogden: Rosa's Cafe. We found it through Yelp. Debbie ordered a smothered pork burrito, and I had a chili relleno. Both were outstanding – they had a home-cooked vibe, much like our beloved Los Primos. The portions were gigantic, especially that burrito. Even better, the staff (allegedly a family) were just as friendly as the folks at Los Primos. We knew it was going to be good when we first opened the door. Debbie stood there for a moment, trying to figure out how to negotiate the small step up into the restaurant. An ample young man who works there stepped out to help with a big smile, and simply lifted her right up. Problem solved! An older man guessed that this was our first time, and advised us on what to get based on our tolerance for spiciness. We placed our order, grabbed some mango Jarritos from the fridge (again, just like Los Primos), and sat down to wait. Less than five minutes later, our food was in front of us. Mine came with rice and refries, and both of those were also outstanding – as was the giant, thick flour tortilla that came with the meal. That tortilla was obviously homemade for those burritos. The beans are made there, and man can you tell. The rice is something that most Mexican restaurants don't do well, with the rice typically grossly overcooked. Not here. The rice was perfect, the sauce beautifully done, and just the right amount of corn, carrots, etc. You can probably guess that we'll be going back. :)
Why am I busy today? I'm catching up on two weeks of neglected financial stuff. It's been accumulating in a pile on my desk, and today I shall demolish that pile...
I squired Debbie down to Ogden for her hair appointment, which took 3.5 hours. She does this every five weeks, so that works out to roughly 40 hours a year. Me, I get a haircut every 5 or 6 months, whether I need it or not. :) My haircuts generally take less than 15 minutes. My haircuts cost $15, including a 50% tip (which the ladies who cut my hair are very happy with!). Debbie's cost ... you don't want to know, especially if you include the cost of the chemical soup she buys to maintain it. Now, I like her hair, mind you. I'm just noting the differences here, and pondering the magnitude of the investment of time and treasure. I cannot even imagine doing this myself...
When we were done with her hair appointment, we tried out a new restaurant in Ogden: Rosa's Cafe. We found it through Yelp. Debbie ordered a smothered pork burrito, and I had a chili relleno. Both were outstanding – they had a home-cooked vibe, much like our beloved Los Primos. The portions were gigantic, especially that burrito. Even better, the staff (allegedly a family) were just as friendly as the folks at Los Primos. We knew it was going to be good when we first opened the door. Debbie stood there for a moment, trying to figure out how to negotiate the small step up into the restaurant. An ample young man who works there stepped out to help with a big smile, and simply lifted her right up. Problem solved! An older man guessed that this was our first time, and advised us on what to get based on our tolerance for spiciness. We placed our order, grabbed some mango Jarritos from the fridge (again, just like Los Primos), and sat down to wait. Less than five minutes later, our food was in front of us. Mine came with rice and refries, and both of those were also outstanding – as was the giant, thick flour tortilla that came with the meal. That tortilla was obviously homemade for those burritos. The beans are made there, and man can you tell. The rice is something that most Mexican restaurants don't do well, with the rice typically grossly overcooked. Not here. The rice was perfect, the sauce beautifully done, and just the right amount of corn, carrots, etc. You can probably guess that we'll be going back. :)
Why am I busy today? I'm catching up on two weeks of neglected financial stuff. It's been accumulating in a pile on my desk, and today I shall demolish that pile...
Friday, April 21, 2017
Paradise ponders, filling stations, muddy dogs, and wet weather ahead edition...
It's now 10 days since Debbie had the hardware removed from her knee, and she's recovering nicely. There was a fairly big incision, and her healing process this time is all about that. She can already put most of her weight on her left knee (the one that was operated on). That incision was closed with staples, and they come out next Wednesday. Once that happens, Debbie should be unleashed on the physical therapy process. So far as we know now, she'll be doing that entirely on her own. We're going to ask next week whether she should have a professional physical therapist work with her on it...
And speaking of Debbie... She can't quite drive on her own yet, as she needs a bit of help getting in and out of the car. But she has a hair appointment today, down in Ogden. So I will be playing chauffeur for part of the day, to get her down there and back. :) We'll most likely eat out somewhere while we're down there – wouldn't want to miss the opportunity!
Thursday, April 20, 2017
Prehistoric computing...
Prehistoric computing... Ken Shirriff does his usual incredibly nerdy computing archaeology...
Tough choices...
Tough choices... The algorithmic trading server I worked on a few years ago used three different numeric types to represent quantities of money (all USD, in its case). We used scaled integers (32 bit scaled by 100) to represent stock prices (trades, bid, and ask) because that was known to be sufficient precision for the task and was fast because those integers are native types. We used scaled longs (64 bits scaled by 10000) for foreign exchange prices (also trades, bid, and ask) for the same reasons. Finally, we used BigDecimal (Java's built-in decimal with arbitrary precision) for aggregate calculations because it was the only built-in decimal type with enough precision, and because calculations like that were relatively infrequent and the performance penalty wasn't too bad.
But using several different types for the same logical purpose had very bad consequences for our system's reliability. Why? Because on every calculation involving money in the entire system, the programmer had to carefully think about the operands, make sure they were in the same value representation, convert them correctly if not, do the calculation, then convert the result (if necessary) to the desired type. At the same time, the programmer had to correctly anticipate and handle any possible overflow.
So how bad could that be? Here's a real-world example from that same algorithmic trading server. Periodically we would look at the bid/ask stack for particular stocks within 5% of the last trade price. For a highly liquid stock that might involve several thousand entries, where each entry was a price and a quantity. We needed to get the sum of the extended price for each entry, and then an average price for the ask stack and separately for the bid stack. The prices were in scaled integers, the quantities also in integers - but their product could exceed what could be held even in our scaled longs. So we had to convert each price and each quantity to a BigDecimal, then do the multiplication to get the extended price. Then we had to sum all those extended prices separately for the bid and ask stack. We could sum the quantities safely in a long, so we did. Then we had to convert that summed quantity to a BigDecimal so we could divide the sum of extended prices by the summed quantity. The result was a BigDecimal, but we needed a scaled integer for the result – so we had to convert it back. That means we needed to (very carefully!) check for overflow, and we also had to set the BigDecimal's rounding mode correctly. Nearly every step of that process had an error in it, due to some oversight on the programmer's part. We spent days tracking those errors down and fixing them. And that's just one of hundreds of similar calculations that one server was doing!
Ideally there would be one way to represent the quantity of money that would use scaled integers when feasible, and arbitrary precision numbers when it wasn't. It's certainly possible to have a single Java class with a single API that “wrapped” several internal representations. This is much easier if the instances of the class are immutable, which would be good design practice in any case. The basic rule for that class at construction time would be to choose the most performant representation that has the precision required. We could have used such a class on that algorithmic trading server, and that would have saved us many errors – but none of us thought of it at the time...
Note: this is the last post of this series on representing and calculating monetary values in Java. I've provided a link for the series at right. If perchance some other semi-coherent thought occurs to me, I reserve the right to add to this mess...
But using several different types for the same logical purpose had very bad consequences for our system's reliability. Why? Because on every calculation involving money in the entire system, the programmer had to carefully think about the operands, make sure they were in the same value representation, convert them correctly if not, do the calculation, then convert the result (if necessary) to the desired type. At the same time, the programmer had to correctly anticipate and handle any possible overflow.
So how bad could that be? Here's a real-world example from that same algorithmic trading server. Periodically we would look at the bid/ask stack for particular stocks within 5% of the last trade price. For a highly liquid stock that might involve several thousand entries, where each entry was a price and a quantity. We needed to get the sum of the extended price for each entry, and then an average price for the ask stack and separately for the bid stack. The prices were in scaled integers, the quantities also in integers - but their product could exceed what could be held even in our scaled longs. So we had to convert each price and each quantity to a BigDecimal, then do the multiplication to get the extended price. Then we had to sum all those extended prices separately for the bid and ask stack. We could sum the quantities safely in a long, so we did. Then we had to convert that summed quantity to a BigDecimal so we could divide the sum of extended prices by the summed quantity. The result was a BigDecimal, but we needed a scaled integer for the result – so we had to convert it back. That means we needed to (very carefully!) check for overflow, and we also had to set the BigDecimal's rounding mode correctly. Nearly every step of that process had an error in it, due to some oversight on the programmer's part. We spent days tracking those errors down and fixing them. And that's just one of hundreds of similar calculations that one server was doing!
Ideally there would be one way to represent the quantity of money that would use scaled integers when feasible, and arbitrary precision numbers when it wasn't. It's certainly possible to have a single Java class with a single API that “wrapped” several internal representations. This is much easier if the instances of the class are immutable, which would be good design practice in any case. The basic rule for that class at construction time would be to choose the most performant representation that has the precision required. We could have used such a class on that algorithmic trading server, and that would have saved us many errors – but none of us thought of it at the time...
Note: this is the last post of this series on representing and calculating monetary values in Java. I've provided a link for the series at right. If perchance some other semi-coherent thought occurs to me, I reserve the right to add to this mess...
Wednesday, April 19, 2017
Storing and transmitting monetary values...
Storing and transmitting monetary values... Most financial applications these days are not standalone applications, but rather components of much larger and more complicated systems. In a past life I was the CTO of a firm that made stock and option trading software, and I once made a map of all the systems that our servers communicated with. There were about a dozen separate machines in our own server room that talked to each other. There were also over two hundred other applications (in over thirty other organizations) that our servers talked to. Those communications paths used a dozen or so different protocols, not counting minor variations. In addition to all these connections, our servers also stored financial information: in memory, on disk, and in logs. That system was not an outlier – I've worked on dozens of other systems just as complex, or even more so.
This complexity has lots of implications when it comes to representing monetary values. What jumps right out to anyone examining all these needs is that there is no “one way” to represent a monetary value that is correct, best, or optimal.
Often the representation has to match an existing standard. For instance, perhaps the monetary value must be in the form of an ASCII string, like this:
When storing or transmitting large numbers of values, often a compact (or compressed) encoding is essential. I once worked on a server that did algorithmic trading (that is, the program decided what stocks to buy and sell). This server needed to store (both on disk and in memory) huge tables of stock pricing data. On busy days this could amount to several hundred million entries. The original design of the server represented the monetary values in a fixed length binary structure that occupied 22 bytes, so on busy days we were storing a couple of gigabytes of data – and moving that data between disk, memory, and CPU cache. We observed that this was a bottleneck in our code, so we came up with a variable-length encoding that averaged just 7.5 bytes per value. We rolled our own on this one, as the numeric representation we were using didn't have a compact encoding. The performance impact was stunning, much more than the 3x you might naively expect. The biggest impact came from fewer CPU cache misses, the second biggest from faster encoding/decoding time. The latter we didn't expect at all. The real lesson for me: compact encodings are very valuable!
Databases present another challenge for representing monetary values. The numeric column types available often can be specified with the precision required – but the API will require converting the value to or from a string or an unlimited precision value (such as BigDecimal). Sometimes the values don't need to be queried, but rather simply stored, as key-accessed blobs. In those cases, a compact encoding is valuable, especially for large tables of values accessed as a whole.
From all this we can derive another requirement for a monetary value representation: flexibility of encodings. There should be a variety of supported, standard encodings including (especially) a compact, variable-length binary encoding, a fixed-length binary encoding. There should be support for conversions to and from unlimited precision numbers as well as native types. There should be support for conversions to and from strings. Also very important, for flexibility: support for adding encodings – because there's no way to anticipate all the strange things the world will require of you...
This complexity has lots of implications when it comes to representing monetary values. What jumps right out to anyone examining all these needs is that there is no “one way” to represent a monetary value that is correct, best, or optimal.
Often the representation has to match an existing standard. For instance, perhaps the monetary value must be in the form of an ASCII string, like this:
$4532.97. The standard might specify that it be in a fixed-length field, with spaces padding to the left as required. Or the standard might specify that the value be in XML, encoded in UTF-16, with a tag of “AMT” for the amount, and “CUR” for the three-character ISO currency code. Some older protocols have specified binary formats, with a numeric code for the currency and packed BCD for the value. I could go on and on with these, because many clever and/or crazy people have devoted a great amount of time to inventing all these schemes.When storing or transmitting large numbers of values, often a compact (or compressed) encoding is essential. I once worked on a server that did algorithmic trading (that is, the program decided what stocks to buy and sell). This server needed to store (both on disk and in memory) huge tables of stock pricing data. On busy days this could amount to several hundred million entries. The original design of the server represented the monetary values in a fixed length binary structure that occupied 22 bytes, so on busy days we were storing a couple of gigabytes of data – and moving that data between disk, memory, and CPU cache. We observed that this was a bottleneck in our code, so we came up with a variable-length encoding that averaged just 7.5 bytes per value. We rolled our own on this one, as the numeric representation we were using didn't have a compact encoding. The performance impact was stunning, much more than the 3x you might naively expect. The biggest impact came from fewer CPU cache misses, the second biggest from faster encoding/decoding time. The latter we didn't expect at all. The real lesson for me: compact encodings are very valuable!
Databases present another challenge for representing monetary values. The numeric column types available often can be specified with the precision required – but the API will require converting the value to or from a string or an unlimited precision value (such as BigDecimal). Sometimes the values don't need to be queried, but rather simply stored, as key-accessed blobs. In those cases, a compact encoding is valuable, especially for large tables of values accessed as a whole.
From all this we can derive another requirement for a monetary value representation: flexibility of encodings. There should be a variety of supported, standard encodings including (especially) a compact, variable-length binary encoding, a fixed-length binary encoding. There should be support for conversions to and from unlimited precision numbers as well as native types. There should be support for conversions to and from strings. Also very important, for flexibility: support for adding encodings – because there's no way to anticipate all the strange things the world will require of you...
Paradise ponders, thermostat monitor, borosilicate glass, and excellent beef soup edition...
Paradise ponders, thermostat monitor, borosilicate glass, and excellent beef soup edition... After all the work we've had done to our downstairs furnace, it still has the original problem that started last December: it cycles on and off every 5 minutes or so. The changes made have greatly increased the air flow, especially in our basement cattery, and that's a very good thing. I'm happy to have made the changes even if they didn't fix the issue. Nevertheless, we still need to find (and fix!) the cause of this rapid cycling.
One of the possible culprits is our Nest thermostat. When the furnace is all buttoned up, there isn't any exterior indication of whether the thermostat is “calling” for heat. So yesterday afternoon I built a thermostat monitor. This is a ridiculously simple piece of electronics: just three pre-packaged 24V (AC or DC) LED monitors. One of them monitors the 24V power to the thermostat, another monitors the “call” signal, and the last one monitors the fan signal. The fan signal is used only when we want to run the fan without heat. I packaged them in a Ziploc food container, and mounted it to the furnace with a magnet. The really important one is the call signal. Here's some photos of my monitor in place:
After I put that in place, I sat and watched two complete cycles of the heater. The call signal never wavered – which tells us that the thermostat is doing its job perfectly, and the problem is somewhere in the heater. In the first photo above, if you embiggen it and look just to the left of those labels, near the bottom of the labels, you'll see a dim neon bulb showing. That is normally solidly on, indicating that all is well. I noticed something last night that we've all managed to miss before. When the heater has been on for a couple of minutes, the burner goes out (gas turned off) while the fan is still going. For the next 30 seconds or so after that, the neon light is blinking a two digit code: 3 short blinks, then 1 long blink, so “31”. Then after the 30 seconds is up, the fan stops and the neon light turns back to solidly on.
That 31 code means a problem in the low pressure sensor. This is a safety device that ensures the exhaust gases are going out the vent and not into the mechanical room – a good thing! My nose doesn't detect any exhaust gases in there, so I suspect the problem is not a lack of draft, but rather a malfunction in that switch. In any case, this is a certifiable clue as to the source of our cycling problem. That means we might actually be able to get it fixed! Yay!
Yesterday was Tuesday, and that means beef soup at Los Primos. Debbie didn't feel up to going out, so I ran up and got two takeout orders of soup. The folks there were disappointed not to see Debbie, and asked after her health. They told me to make sure she shows up next Tuesday. :) The food there is really special, but the people at the family-owned restaurant are even more so...
A few months ago, we bought eight of these tumblers. I thought I'd posted about them earlier, but I can't find anything on them. Debbie and I both tend to drink big glasses of stuff: water, milk, iced tea, and the like. Cold drinks, mostly, and often iced. These tumblers caught my eye because they're insulated – there's two layers of glass with a vacuum between them, just like an old-fashioned vacuum thermos bottle. Plus they're big: 20 ounces. The glasses are made from borosilicate glass, a material I know well for its unusual combination of strength and low thermal expansion coefficient. It's also very clear. The fact that they have a low thermal expansion coefficient means they're safe for both hot and cold drinks, plus you can throw them in the dishwasher. We've been using them for all our cold drinks, and we both love them. I'm especially appreciative of the rounded rim (comfortable in my mouth) and the sturdiness – we still have all 8 of them, despite daily use for 3 or 4 months now. Looking on the Amazon page I see that there are a few very negative (one star) reviews, mainly for three reasons: their weight, the thickness of the rim, and their alleged fragility. We actually like the weight and the thick rim, and I'm guessing that most people do as the reviews are overwhelmingly positive. As to the fragility, I can only say that these are lasting longer than the majority of glassware we own. :) Anyway, these are resoundingly endorsed by the Dilatushes of Paradise!
One of the possible culprits is our Nest thermostat. When the furnace is all buttoned up, there isn't any exterior indication of whether the thermostat is “calling” for heat. So yesterday afternoon I built a thermostat monitor. This is a ridiculously simple piece of electronics: just three pre-packaged 24V (AC or DC) LED monitors. One of them monitors the 24V power to the thermostat, another monitors the “call” signal, and the last one monitors the fan signal. The fan signal is used only when we want to run the fan without heat. I packaged them in a Ziploc food container, and mounted it to the furnace with a magnet. The really important one is the call signal. Here's some photos of my monitor in place:
After I put that in place, I sat and watched two complete cycles of the heater. The call signal never wavered – which tells us that the thermostat is doing its job perfectly, and the problem is somewhere in the heater. In the first photo above, if you embiggen it and look just to the left of those labels, near the bottom of the labels, you'll see a dim neon bulb showing. That is normally solidly on, indicating that all is well. I noticed something last night that we've all managed to miss before. When the heater has been on for a couple of minutes, the burner goes out (gas turned off) while the fan is still going. For the next 30 seconds or so after that, the neon light is blinking a two digit code: 3 short blinks, then 1 long blink, so “31”. Then after the 30 seconds is up, the fan stops and the neon light turns back to solidly on.
That 31 code means a problem in the low pressure sensor. This is a safety device that ensures the exhaust gases are going out the vent and not into the mechanical room – a good thing! My nose doesn't detect any exhaust gases in there, so I suspect the problem is not a lack of draft, but rather a malfunction in that switch. In any case, this is a certifiable clue as to the source of our cycling problem. That means we might actually be able to get it fixed! Yay!
Yesterday was Tuesday, and that means beef soup at Los Primos. Debbie didn't feel up to going out, so I ran up and got two takeout orders of soup. The folks there were disappointed not to see Debbie, and asked after her health. They told me to make sure she shows up next Tuesday. :) The food there is really special, but the people at the family-owned restaurant are even more so...
Tuesday, April 18, 2017
Inexact results and monetary calculations...
Inexact results and monetary calculations... There are a few things worth pondering about making calculations with money where the results are not exact quantities.
Consider the case of inexact results that are expected to be inexact. A common example of this is a compound interest calculation that involves logarithms, powers, and roots – not much chance of an exact answer on those! In cases like this, what we need for money is for the answer to be rounded to the nearest conventional unit of money (for instance, the nearest penny in USD). This is, however, a bit more complicated than you might think.
Consider a case in USD, where we want to round to the nearest penny. Suppose our unrounded result was 0.121 – that's easy, the rounded result is 0.12, rounded down (toward zero). Similarly, 0.346 would rounded up to 0.35. Both of those are obvious and uncontroversial. But suppose our unrounded result was 0.115? Do we round that down to 0.11, or up to 0.12? In both cases, the difference between the rounded and unrounded values is the same: 0.05. How do we choose between rounding up or rounding down?
Most of us old enough to predate the “new math” were taught in elementary school to round such values up, all the time. I have no idea what the hell kids are taught these days, except I'm confident it's not very useful. However, always rounding halfway values up over a large number of results introduces a bias toward larger average results. Bankers and their customers noticed this a long, long time ago. Some clever accountants came up with a simple solution that's easy to implement and removes the bias: “half even” rounding. In this kind of rounding, a result like 0.115 is rounded so that the next most significant digit is rounded to an even value – so round up to 0.12 in this example, because 2 is even and 3 is not. If the unrounded result was 0.165, though, then we'd round down to 0.16, because 6 is even. I should note that one could also use a “half odd” rounding to accomplish the same thing.
In some kinds of financial calculations, though, even this solution isn't what's needed. For instance, in certain kinds of models you always want to round toward zero. There are a half-dozen or so different kinds of rounding that are occasionally useful in monetary calculations. The way monetary quantities are represented really needs to support all of these rounding flavors.
Now lets consider a different case: where results are expected to be exact, and an inexact result indicates a mistake of some kind. I ran into a case like this in a stock trading application, where we multiplied the number of shares bought or sold times the sales price to get a “lot price”. Since shares of stock are indivisible (e.g., you can't buy 1.5 shares of IBM), that result should always be exact, to the penny. If it's inexact, then something is wrong – perhaps someone mistakenly entered a fractional share quantity, or there's a bug in the program. For these sorts of situations, it is very useful to know whether a monetary quantity is exact or inexact (e.g., has been rounded). The way monetary quantities are represented should support this.
Finally, sometimes in monetary calculations we really don't want inexact values to be rounded. For example, suppose we had 10,000 USD that we want to divide in thirds and distribute to three accounts. The rounded, inexact result of that would be 3,333.33 USD that we put into each account – but that only adds up to 9,999.99 USD – we “lost” a penny and now our books are out of whack. The way financial applications generally solve problems of this type is to use some algorithm to choose a lucky account, and they give that account the extra penny (in this case). These algorithms themselves are interesting, as they need to be repeatable (so you can't just roll the dice) for audits, but they are not the problem I'm discussing here. It's knowing that we have an inexact result, and how much is “left over” to distribute that I care about today.
This sort of problem always has a division operation at the root of it. The general solution is really simple: you need a division operation that gives you the floor of the quotient, and the remainder. So the result of the division in the example above would be 3,333.33 with a remainder of 0.01. The way monetary quantities are represented must include the division-with-remainder operation. Ideally it would allow returning quotients that are floor, ceiling, nearest toward zero, or nearest away from zero (all with appropriately adjusted remainders) because all of these are useful in some financial applications.
Consider the case of inexact results that are expected to be inexact. A common example of this is a compound interest calculation that involves logarithms, powers, and roots – not much chance of an exact answer on those! In cases like this, what we need for money is for the answer to be rounded to the nearest conventional unit of money (for instance, the nearest penny in USD). This is, however, a bit more complicated than you might think.
Consider a case in USD, where we want to round to the nearest penny. Suppose our unrounded result was 0.121 – that's easy, the rounded result is 0.12, rounded down (toward zero). Similarly, 0.346 would rounded up to 0.35. Both of those are obvious and uncontroversial. But suppose our unrounded result was 0.115? Do we round that down to 0.11, or up to 0.12? In both cases, the difference between the rounded and unrounded values is the same: 0.05. How do we choose between rounding up or rounding down?
Most of us old enough to predate the “new math” were taught in elementary school to round such values up, all the time. I have no idea what the hell kids are taught these days, except I'm confident it's not very useful. However, always rounding halfway values up over a large number of results introduces a bias toward larger average results. Bankers and their customers noticed this a long, long time ago. Some clever accountants came up with a simple solution that's easy to implement and removes the bias: “half even” rounding. In this kind of rounding, a result like 0.115 is rounded so that the next most significant digit is rounded to an even value – so round up to 0.12 in this example, because 2 is even and 3 is not. If the unrounded result was 0.165, though, then we'd round down to 0.16, because 6 is even. I should note that one could also use a “half odd” rounding to accomplish the same thing.
In some kinds of financial calculations, though, even this solution isn't what's needed. For instance, in certain kinds of models you always want to round toward zero. There are a half-dozen or so different kinds of rounding that are occasionally useful in monetary calculations. The way monetary quantities are represented really needs to support all of these rounding flavors.
Now lets consider a different case: where results are expected to be exact, and an inexact result indicates a mistake of some kind. I ran into a case like this in a stock trading application, where we multiplied the number of shares bought or sold times the sales price to get a “lot price”. Since shares of stock are indivisible (e.g., you can't buy 1.5 shares of IBM), that result should always be exact, to the penny. If it's inexact, then something is wrong – perhaps someone mistakenly entered a fractional share quantity, or there's a bug in the program. For these sorts of situations, it is very useful to know whether a monetary quantity is exact or inexact (e.g., has been rounded). The way monetary quantities are represented should support this.
Finally, sometimes in monetary calculations we really don't want inexact values to be rounded. For example, suppose we had 10,000 USD that we want to divide in thirds and distribute to three accounts. The rounded, inexact result of that would be 3,333.33 USD that we put into each account – but that only adds up to 9,999.99 USD – we “lost” a penny and now our books are out of whack. The way financial applications generally solve problems of this type is to use some algorithm to choose a lucky account, and they give that account the extra penny (in this case). These algorithms themselves are interesting, as they need to be repeatable (so you can't just roll the dice) for audits, but they are not the problem I'm discussing here. It's knowing that we have an inexact result, and how much is “left over” to distribute that I care about today.
This sort of problem always has a division operation at the root of it. The general solution is really simple: you need a division operation that gives you the floor of the quotient, and the remainder. So the result of the division in the example above would be 3,333.33 with a remainder of 0.01. The way monetary quantities are represented must include the division-with-remainder operation. Ideally it would allow returning quotients that are floor, ceiling, nearest toward zero, or nearest away from zero (all with appropriately adjusted remainders) because all of these are useful in some financial applications.
Paradise ponders, filling station, fuzzy eyeballs, and giant wrench edition...
Paradise ponders, filling station, fuzzy eyeballs, and giant wrench edition... Yesterday was another really busy day around the place. I got dragged away from my own projects several times to help the guys working on our “filling station”. There were decisions to make, some education on how the components worked, tools to lend, and hardware to scrounge for.
In the first photo below, Joe is using a fancy core drill (with a water-cooled diamond bit!) to drill holes through the back wall of the filling station. These holes allow the two pieces of 1" black iron pipe through the wall. I'll be grouting them later to make them water-tight. One of the pipes is for gasoline, the other for diesel. The second photo shows the inside of the filling station, with most of the plumbing done. The fuel comes in through the pipes on the bottom, then on each leg (for each fuel) goes through a shutoff valve, a filter/water separator, and a gauge. The pipes on top will be extended toward the opening, where a swiveled hose with a nozzle will be attached. The other end of the pipes is currently just open underneath the tanks; there's a bit of plumbing left to get done there, too. But look at all that lovely progress! I think that by next week I should be calling the local petroleum distributor to order me up some fuel. Woo hoo!
Yesterday Debbie and I took a jaunt up to our optometrist to pick up her reworked new glasses. The first time we got them she was getting headaches when wearing them. When we took them back, we discovered that the optometrist had made a prescription mistake. He wrote it as 53° axis (for astigmatism), but it was supposed to be 153°! They immediately ordered new lenses for her, and yesterday we got them. Her first reaction: she couldn't see well at distance. Now she's got to wear them for a week to see if her eyeballs will relax so she can see well with them. If not, it's back to the optometrist we go – for round three!
Mark T. was here yesterday to finish up putting the risers. There was a bit of a holdup, though, as he was trying to remove our old aluminum riser heads from the PVC pipe that holds them. The pipe is thick-walled 3" ID PVC, male threaded, and the riser screws onto the pipe. Well, these old riser heads had been in place for 20 years or so, and they weren't going to come off easily. Mark only had one pipe wrench big enough to grip them, and that one just barely. So I grabbed my giant water pump wrench, which has jaw that open to 5" (commercial photo at right). I don't often need something that big, but when I do it's really hard to beat this thing. It's got gripping power every bit as good as a conventional pipe wrench, but it's much easier to use. Mark and I got those things apart in no time. :)
In the first photo below, Joe is using a fancy core drill (with a water-cooled diamond bit!) to drill holes through the back wall of the filling station. These holes allow the two pieces of 1" black iron pipe through the wall. I'll be grouting them later to make them water-tight. One of the pipes is for gasoline, the other for diesel. The second photo shows the inside of the filling station, with most of the plumbing done. The fuel comes in through the pipes on the bottom, then on each leg (for each fuel) goes through a shutoff valve, a filter/water separator, and a gauge. The pipes on top will be extended toward the opening, where a swiveled hose with a nozzle will be attached. The other end of the pipes is currently just open underneath the tanks; there's a bit of plumbing left to get done there, too. But look at all that lovely progress! I think that by next week I should be calling the local petroleum distributor to order me up some fuel. Woo hoo!
Yesterday Debbie and I took a jaunt up to our optometrist to pick up her reworked new glasses. The first time we got them she was getting headaches when wearing them. When we took them back, we discovered that the optometrist had made a prescription mistake. He wrote it as 53° axis (for astigmatism), but it was supposed to be 153°! They immediately ordered new lenses for her, and yesterday we got them. Her first reaction: she couldn't see well at distance. Now she's got to wear them for a week to see if her eyeballs will relax so she can see well with them. If not, it's back to the optometrist we go – for round three!
Monday, April 17, 2017
Things that go wrong with monetary calculations...
Things that go wrong with monetary calculations... As a programmer, it's very easy to forget about the error-producing “edge cases” in calculations. These are all things that can occur in any calculations, including monetary calculations. For a robust financial application, all of these must be handled in some way. The big three:
- Division by zero. This is probably the classic “gotcha” in financial calculations, probably because there are so many ways for it to happen that programmers somehow fail to foresee. The standard floating point implementations will return a value of infinity for this operation (either positive or negative). Some libraries will throw an exception. Either method works.
- Invalid operation. The canonical examples are zero divided by zero, or the square root of a negative number. There are others, too. I've had this error crop up in several implementations of bond and stock options models I made. The standard floating point implementations will return a value of Not A Number (abbreviated as NaN) for these operations. Other libraries will throw an exception. Again, either method works.
- Inexact result. An inexact result occurs when the result of any calculation cannot be represented exactly because the number representation cannot hold either the number of significant digits or the exponent size, or both. In either binary or decimal, the result of 1/3 is one example of such a result. Standard floating point implementations silently round such results, providing no indication that the result is inexact.
Paradise ponders, walks and drives edition...
Paradise ponders, walks and drives edition... Yesterday afternoon I took Mako (our giant field spaniel puppy) for a walk up my usual route, 1.5 miles round trip. It was an absolutely gorgeous day, as you can see in the photos below. Spring is springing, and green is popping out all over. I tied Mako to a fence post to take these photos, and as you can see in the first photo he had himself all wrapped up within seconds!
Mako had an adventure on this walk that neither of us expected. He behaves a lot like Mo'i used to, snuffling along through the grasses in search of something he can eat (a vole or mouse, perhaps). Yesterday he came across a hole about 8" in diameter, hidden in the grass. Before I knew what was happening, he had his head in it right down to his shoulders. A second or so later he came flying backwards out of the hole, followed quickly by a spittin' mad groundhog. That old ground hog charged Mako fearlessly, and looked damned effective with his teeth and claws. Mako tumbled backwards and out of range, then promptly pooped. :) When we continued our walk, he gave that groundhog hole very wide berth!
I saw two other interesting animals on our walk: a white-tailed kite and a very grey red fox. Those kites are beautiful birds that were quite common where we used to live in California. This is the first one I've seen here. It hovered for five minutes or so in a few locations nearly straight overhead, so I had some excellent viewing. The fox we've seen before; apparently these fields are well within its territory. Cover is scarce right now, with the alfalfa just barely emerging, so the chances of spotting the fox now are much higher. Mako never saw either animal. :)
When I got back from the walk, Debbie and I took a drive out toward Hardware Ranch, and then a few miles up Ant Flats Road. We took the Tesla, and the bumpy Ant Flats Road was a challenge for her because of the pain in her knee's incision. We probably won't do that again for a few weeks, until she's feeling better. But ... we did see some animals, especially birds: a golden eagle, Sandhill cranes, blue herons, a pheasant, and lots of deer. The right-hand fork of Blacksmith Fork River was running at around 8x normal volume, so the waterfalls along the way were really pretty (photos below).
The first photo is of a man-made water feature in the front yard of the cabin on Miller's Ranch. They get to look at this out their windows. The other photos are two angles of the same natural falls, just a mile or so from Hardware Ranch along Ant Flats Road. We've been by this dozens of times, so we're very familiar with its normal flow – a small fraction of what you see here.
Mako had an adventure on this walk that neither of us expected. He behaves a lot like Mo'i used to, snuffling along through the grasses in search of something he can eat (a vole or mouse, perhaps). Yesterday he came across a hole about 8" in diameter, hidden in the grass. Before I knew what was happening, he had his head in it right down to his shoulders. A second or so later he came flying backwards out of the hole, followed quickly by a spittin' mad groundhog. That old ground hog charged Mako fearlessly, and looked damned effective with his teeth and claws. Mako tumbled backwards and out of range, then promptly pooped. :) When we continued our walk, he gave that groundhog hole very wide berth!
I saw two other interesting animals on our walk: a white-tailed kite and a very grey red fox. Those kites are beautiful birds that were quite common where we used to live in California. This is the first one I've seen here. It hovered for five minutes or so in a few locations nearly straight overhead, so I had some excellent viewing. The fox we've seen before; apparently these fields are well within its territory. Cover is scarce right now, with the alfalfa just barely emerging, so the chances of spotting the fox now are much higher. Mako never saw either animal. :)
When I got back from the walk, Debbie and I took a drive out toward Hardware Ranch, and then a few miles up Ant Flats Road. We took the Tesla, and the bumpy Ant Flats Road was a challenge for her because of the pain in her knee's incision. We probably won't do that again for a few weeks, until she's feeling better. But ... we did see some animals, especially birds: a golden eagle, Sandhill cranes, blue herons, a pheasant, and lots of deer. The right-hand fork of Blacksmith Fork River was running at around 8x normal volume, so the waterfalls along the way were really pretty (photos below).
The first photo is of a man-made water feature in the front yard of the cabin on Miller's Ranch. They get to look at this out their windows. The other photos are two angles of the same natural falls, just a mile or so from Hardware Ranch along Ant Flats Road. We've been by this dozens of times, so we're very familiar with its normal flow – a small fraction of what you see here.
Sunday, April 16, 2017
Chicken pot pie...
These deviations from the recipe had another result as well: we ended up with twice as much filling as we were supposed to. I ended up vacuum-bagging (for freezing) half the filling, and baking the rest with the puff pastry top. When it was done, we tucked into it with enthusiasm and managed to put away about 1/3 of that pan. Debbie actually had more than I did! I took about half the rest and put it in a refrigerator container. The remainder is now in two more vacuum-bags, waiting to cool down before I vacuum them and toss them in the freezer. We have much (yummy!) chicken pot pie in our future!
While I was cooking this, I had to add quite a bit of broth and cream to get enough liquid (because we added so much good stuff). The sauce is thickened with a roux, and I hadn't changed that from the recipe. That meant the sauce was way too thin, so I whipped up some more butter-and-flour roux in a little frying pan. That worked great – when I threw that roux in, the sauce thickened right up. I like the flavor and texture of a roux way better than cornstarch, so I was glad I did it that way...
How about scaled integers for monetary amounts?
How about scaled integers for monetary amounts? A friend recently wondered why I wouldn't simply use scaled integers for monetary amounts. For instance, if I determined that all I needed was 10 significant integer digits, plus 4 decimal places, then I could exactly represent any decimal value within that range by multiplying it times 10,000 and using the resulting integer. For example, I could represent 382.03 as 3,820,300. When it came time to present that number to a human, I'd just divide by 10,000.
Scaled integers work particularly well for addition and subtraction, and for many financial applications that's the bulk of what they do. Consider this addition example, unscaled on the left and scaled by 10,000 on the right:
Multiplies aren't quite as lovely, though. The scale factor gets multiplied along with the actual number, so you get a result that has to be divided by the scale factor to get a correctly scaled result. Example:
And then there's division, where the scale factor essentially is canceled out – requiring you to multiply the result by the scale factor to re-scale it.
If these numbers at our desired precision all fit into a native integer type, this would be a bit unwieldy, a little less performant than native, but workable. In an earlier post I figured that we needed a range that encompassed at least 30 decimal digits just to represent amounts of money. The binary equivalent of 30 decimal digits is about 100 bits. The largest native integer in Java (the long) has 63 significant bits – not even close.
Well, what if we used two longs? That would give us 126 significant bits – plenty of room. Addition and subtraction are still simple with this scheme. Multiplication is a bit harder, but still workable. Division is a bear, though, and substantially slower than a native implementation. Those aren't necessarily deal-killers, just a consideration. A similar issue arises from the fact that with this scheme it takes 16 bytes to store any number. That's expensive in database, mass storage, network transmission, and CPU cache (for any application that uses lots of values, i.e. most of them). But still not necessarily a deal killer.
But, as my mother-in-law would say, there's a worser problem with scaled integers. It derives from the fact that you don't just represent monetary values in an application – you also do math with them. I've used the simple example of multiplying price times quantity to get extended price, but many financial applications do much more than such simple math.
Just to pick one example out of my checkered past: I once was charged with building applications that modeled the performance of complex bonds (that is, those with fancy terms in them, not just simple interest), over wide ranges of multiple environmental variables (LIBOR rate, inflation rate, etc.) in combination with each other. These models had multi-dimensional tables with millions of entries, each of which contained a calculated probable value. In some of the models I built, these values could be as small as 10^-10, with around 8 significant digits. That's not something exotic and unusual, either – it's a perfectly normal sort of financial application.
Here's the real point, though: financial applications need to do math with money, and we really can't predict what the range of numbers they'll need will be. This point has been driven home for me by a number of bad experiences out in that pesky real world. Every application I've ever worked on that used fixed point numeric representation (which scaled integers are an example of) has run into problems with the range of numbers they could represent. The failure modes can be very bad, too – especially if the fixed point implementations aren't good at catching overflows (and many of them don't even try, because of the performance penalty).
This hard stop on the range of numeric values held is the real deal-killer for me with fixed point representations. The performance and size issues just make it a little bit worse. In my opinion, fixed point representation and manipulation of monetary values is a dangerous source of fragility in financial applications. Further, it's one that is very difficult to repair – once the decision to use a particular fixed point representation is made, that decision creates tendrils of dependency that find their way into every nook and cranny of the application.
So how do you avoid this? There's a good solution, but it comes with its own costs: decimal floating point. That will be the subject of a few more posts...
Scaled integers work particularly well for addition and subtraction, and for many financial applications that's the bulk of what they do. Consider this addition example, unscaled on the left and scaled by 10,000 on the right:
773.32 7733200
27.99 279900
------ ------- 801.31 8013100
Multiplies aren't quite as lovely, though. The scale factor gets multiplied along with the actual number, so you get a result that has to be divided by the scale factor to get a correctly scaled result. Example:
4.45 44500
6.02 60200
------ ---------- 26.789 2678900000 rescaled to 267890 And then there's division, where the scale factor essentially is canceled out – requiring you to multiply the result by the scale factor to re-scale it.
773.32 7733200
27.99 279900
------ ------- 27.63 27.63 rescaled to 276300 (results are rounded)
If these numbers at our desired precision all fit into a native integer type, this would be a bit unwieldy, a little less performant than native, but workable. In an earlier post I figured that we needed a range that encompassed at least 30 decimal digits just to represent amounts of money. The binary equivalent of 30 decimal digits is about 100 bits. The largest native integer in Java (the long) has 63 significant bits – not even close.
Well, what if we used two longs? That would give us 126 significant bits – plenty of room. Addition and subtraction are still simple with this scheme. Multiplication is a bit harder, but still workable. Division is a bear, though, and substantially slower than a native implementation. Those aren't necessarily deal-killers, just a consideration. A similar issue arises from the fact that with this scheme it takes 16 bytes to store any number. That's expensive in database, mass storage, network transmission, and CPU cache (for any application that uses lots of values, i.e. most of them). But still not necessarily a deal killer.
But, as my mother-in-law would say, there's a worser problem with scaled integers. It derives from the fact that you don't just represent monetary values in an application – you also do math with them. I've used the simple example of multiplying price times quantity to get extended price, but many financial applications do much more than such simple math.
Just to pick one example out of my checkered past: I once was charged with building applications that modeled the performance of complex bonds (that is, those with fancy terms in them, not just simple interest), over wide ranges of multiple environmental variables (LIBOR rate, inflation rate, etc.) in combination with each other. These models had multi-dimensional tables with millions of entries, each of which contained a calculated probable value. In some of the models I built, these values could be as small as 10^-10, with around 8 significant digits. That's not something exotic and unusual, either – it's a perfectly normal sort of financial application.
Here's the real point, though: financial applications need to do math with money, and we really can't predict what the range of numbers they'll need will be. This point has been driven home for me by a number of bad experiences out in that pesky real world. Every application I've ever worked on that used fixed point numeric representation (which scaled integers are an example of) has run into problems with the range of numbers they could represent. The failure modes can be very bad, too – especially if the fixed point implementations aren't good at catching overflows (and many of them don't even try, because of the performance penalty).
This hard stop on the range of numeric values held is the real deal-killer for me with fixed point representations. The performance and size issues just make it a little bit worse. In my opinion, fixed point representation and manipulation of monetary values is a dangerous source of fragility in financial applications. Further, it's one that is very difficult to repair – once the decision to use a particular fixed point representation is made, that decision creates tendrils of dependency that find their way into every nook and cranny of the application.
So how do you avoid this? There's a good solution, but it comes with its own costs: decimal floating point. That will be the subject of a few more posts...
Paradise ponders, recoveries, flowers, stairs, and risers edition...
Paradise ponders, recoveries, flowers, stairs, and risers edition... Debbie had a milestone day yesterday for her post-surgery recovery. Her bandages came off in the morning (she couldn't do it – got queasy – so I did it for her :). Then she took a shower; oh, so good. Then she got down the stairs to our basement cattery to see her babies. Then we had a steak dinner. Then we went up to Aggie's Creamery and got ice cream cones. A great day for her! But she was tired for some reason after all that. :)
We've got a few flowers in our yard. The daffodils have started to bloom, and then the ground cover (at right) we have in several places is also out. After all the destruction of our yard last year (and continuing this year), I'm amazed anything at all has survived. The sweet peas are starting to come up, too – probably another two or three weeks and they'll be a big burst of color to the west of our house...
Yesterday I completed the installation of the stairs I built into our sun room (photos below). All my careful measuring paid off: the stairs fit perfectly on the first try. The landing is level with our bedroom floor, as intended, and the little “lip” I machined out fit over the door sill exactly as intended. I'm very pleased with the way the finish blends with our tile floor, too. Next step: some more careful measurements for the rail (it will be on the left side). Once I make those, I'll send them off to the folks at Lazy K Wrought Iron to get a rail made. At that point our sun room will (finally!) be complete. We'll make another road trip up there to get them!
Mark T., Dave, and Dave's three sons were here all day yesterday installing 6" diameter irrigation pipe to move the line of risers that used to be in the middle of our back yard to just outside the fence. The new line of risers (visible if you embiggen the photo at right) is a couple of feet onto the property of our friend and neighbor Tim D. Once my sprinklers are installed (that's the next thing Mark T. will be working on), I won't need them at all – but Tim will, to irrigate the 2.5 acre field to the left (north) in the photo. It's a big chunk of work to move all that, and Mark and his helpers did a really nice job of it. The only bit they have left is the easy part: gluing the risers in place onto those vertical 3" pipes. Then it's on to the sprinklers in our yard!
Yesterday I completed the installation of the stairs I built into our sun room (photos below). All my careful measuring paid off: the stairs fit perfectly on the first try. The landing is level with our bedroom floor, as intended, and the little “lip” I machined out fit over the door sill exactly as intended. I'm very pleased with the way the finish blends with our tile floor, too. Next step: some more careful measurements for the rail (it will be on the left side). Once I make those, I'll send them off to the folks at Lazy K Wrought Iron to get a rail made. At that point our sun room will (finally!) be complete. We'll make another road trip up there to get them!
Subscribe to:
Posts (Atom)